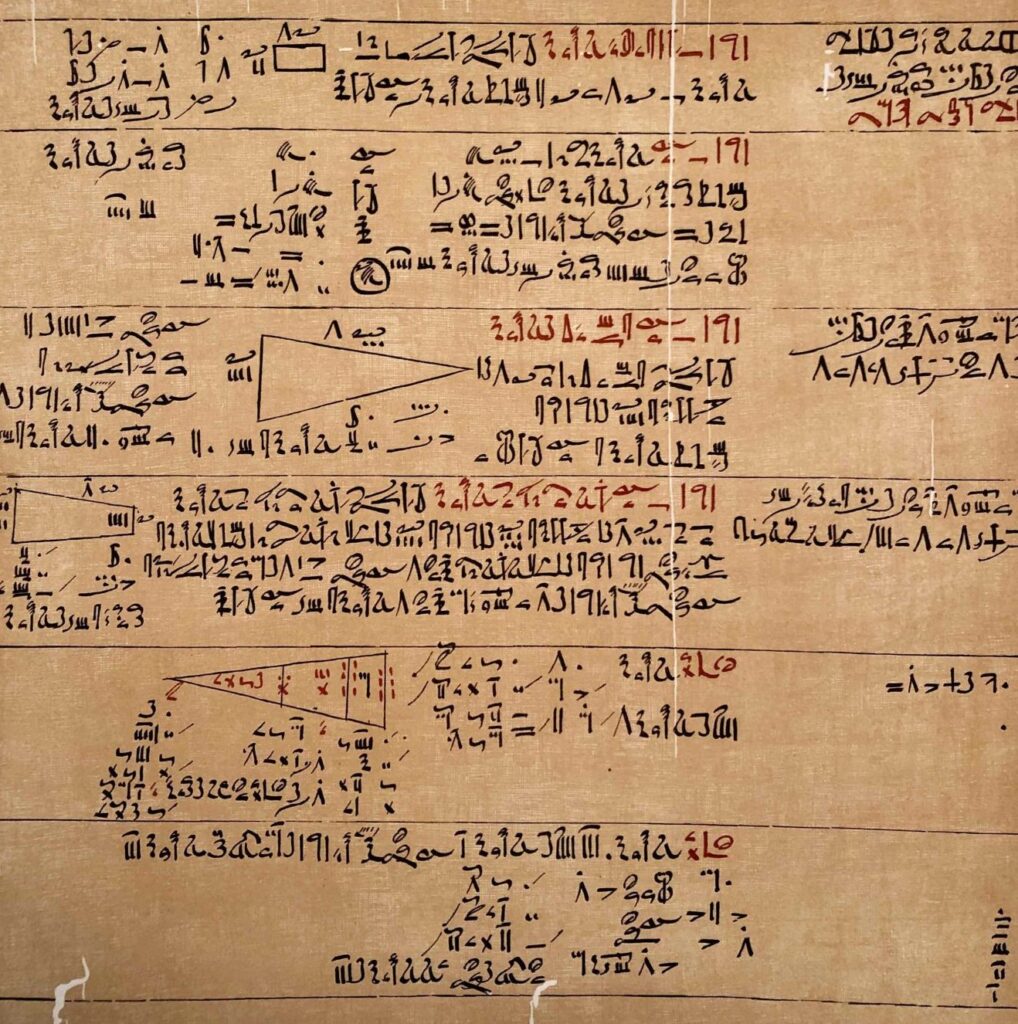
Facsimile van het mathematische papyrus Rhind uit het British Museum in Londen
Onze kennis over de Egyptische rekenkunst is gebaseerd op slechts een klein aantal documenten. Een van de belangrijkste bronnen is papyrus Rhind, die in het British Museum wordt bewaard. Deze papyrus werd in 1858 ontdekt door de Schotse egyptoloog Alexander Henry Rhind in de ruïnes van een klein bouwwerk vlak bij het Ramesseum. Het British Museum verwierf het document uit zijn nalatenschap in 1865. De in het hiëratisch schrift geschreven papyrus is opgesteld door de schrijver Ahmose. Dit moet zijn gebeurd tijdens de 15de dynastie, onder de regering van de Hyksos-koning Apophis. Ahmose vermeldt echter dat hij een 200 jaar ouder document heeft overgeschreven. Dat zou betekenen dat de originele tekst is opgesteld rond 1850 v.Chr., ten tijde van Senwosret III uit de 12de dynastie. De papyrus is een enkele rol met een lengte van 5,5 meter en een breedte van 32 centimeter.
De tekst vangt aan met de belofte dat de lezer ervan belangrijke zaken voorgeschoteld zal krijgen, namelijk ‘een grondige studie van alle dingen, inzicht in alles wat bestaat, en kennis van alle duistere geheimen’. In werkelijkheid bevat het document allerlei wiskundige begrippen, methoden en symbolen en 87 wiskundige problemen en hun oplossingen. Het gaat daarbij om rekenproblemen zoals het verdelen van een aantal broden over een aantal mensen. Ook wordt gezocht naar een methode om de oppervlakte van een driehoek te meten. De oppervlakte van een cirkel met een middellijn 9 wordt benaderd door een vierkant met een zijde 8, wat de waarde van π gelijkstelt aan: (4/3) = 3,16049… Uit de papyrus Rhind weten we ook dat de Egyptenaren alle breuken (met uitzondering van 2/3) uitdrukten als som van verschillende stambreuken, dus breuken met teller 1.
De uit Vlaanderen afkomstige docent klassieke talen, Paul de Zutter, schreef op zaterdag 17 september 2022 het volgende bericht op zijn pagina van de website LinkedIn.
Oude Grieken versus Oude Egyptenaren
Het moet gezegd: de grote Griekse wiskundige en wijsgeer Pythagoras (ca. 570 – 500 v.Chr.) halen we best even van zijn stelling. Die had – bij wijze van spreken – “de stelling van IMHOTEP” moeten heten! Vandaag de dag beschikken we over enkele oud-Egyptische wiskundige papyri van meer dan 4000 jaar oud. De bestudering van één daarvan, de zgn. ‘Rhind-papyrus’, toonde aan dat de bouwmeesters van de farao’s niet alleen vertrouwd waren met complexe mathematische problemen; in hun ontwerpen maakten ze eveneens gebruikt van – jawel – de stelling van Pythagoras, en dit zo’n 1000 jaar vooraleer deze op schrift werd gesteld. Pythagoras pikte ze als het ware tijdens een Nijlcruise uit een tempelarchief op. De snoodaard!
Ere wie ere toekomt, dus. Toch mag men de betekenis en het belang van Pythagoras ‘cum suis’ niet geringschatten: de Oude Grieken hebben als eersten de oeroude wijsheden van de mensheid op vlak van mathematica en astronomie gesystematiseerd en voor het westen toegankelijk gemaakt. En wat hen onderscheidde van diegenen bij wie ze de mosterd haalden, was zonder meer hun ingesteldheid. Want waar wetenschappen voor de Babyloniërs en Egyptenaren louter een praktisch doel dienden, beoefenden de Grieken deze uit bewondering vóór en omwille van de wetenschap zelve: “l’art pour l’art” oftewel de “libido sciendi” (W. Van Rooy). Is er een mooiere modus vivendi denkbaar?
